이번 포스트에서는 이진 탐색 트리에 대해 알아본다.
<C++로 쉽게 풀어쓴 자료구조>를 참고하여 작성되었다.
이진 탐색 트리에 대해 알아보기 전에, 빅오 표기법(Big-O)에 대해 간단히 알아보자.
빅오 표기법은 특정한 알고리즘의 시간 복잡도를 표시하는 방법을 말한다. 조금 쉽게 풀이해보자. 예를 들어 어떤 알고리즘을 연산하기 위해서
T(n) = n2 + n + 1
만큼의 연산이 실행된다고 가정한다. n은 입력의 개수 또는 문제의 크기를 의미하는데, 이를테면 a번을 반복하며 1부터 a까지 곱해주는 for문이 있다고 했을 때 a를 n이라고 생각하면 된다.
for(int i=1; i<=a; i++) {
mul *= i } // 이 알고리즘에서 입력의 개수는 a이다.
이 T(n) 함수는 n이 작을 때는 모든 항이 비슷한 영향력을 갖지만, n의 크기가 커질수록 차수가 가장 큰 항의 영향력이 커진다.
n=1일 경우: T(n) = 1 + 1 + 1 = 3
n=100일 경우: T(n) = 10000 + 100 + 1 = 10101(여기서 n2항은 99%의 영향력을 갖는다.)
빅오 표기법은 연산량에 절대적인 영향력을 끼치는 n2만을 중요하게 보고, 다른 항은 없는 것으로 취급한다.
따라서 T(n)의 시간 복잡도는 O(n2)이다.
그렇다면 시간 복잡도가 얼마일 때 좋은 알고리즘일까?
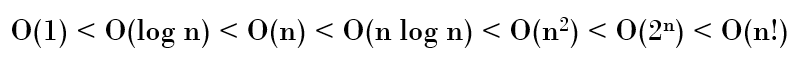
이러한 순서로 좋다고 알려져 있다(참고로 컴퓨터 분야에서 log n은 log2 n을 뜻한다).
실제로 n log n까지는 괜찮은 알고리즘이다. n2부터는 연산량이 급격히 상승하므로 좋은 성능은 아니지만 어쩔 수 없이 사용할 때도 있다. 그러나 2n부터는 사용할 수 없다.
이진 탐색 트리란?

이진 탐색 트리(BST, Binary Search Tree)란 탐색에 최적화된 이진트리 기반의 자료구조로, 아래의 성질을 만족하는 트리를 말한다.
모든 노드는 유일한 키를 갖는다.
왼쪽 서브트리의 키들은 루트의 키보다 작다.
오른쪽 서브트리의 키들은 루트의 키보다 크다.
왼쪽과 오른쪽 서브트리도 이진탐색 트리이다.
이진 탐색 트리는 왜 효율적인가?
탐색 작업은 어디서든 활용할 수 있는 중요한 응용분야지만, 여기서는 스케줄링 문제를 예시로 들어 BST가 효율적인 이유를 설명하겠다.
당신의 하루 일정을 스케줄링한다고 상상해 보자. 이미 당신의 하루는 해야할 일들로 어느정도 채워져 있을 것이다. 그런데 만약 2시에 친구와 약속을 새로 잡고 싶다면 어떻게 할까? 우선 일정표를 탐색하여 2시에 일정이 있는지 확인할 것이다. 일정이 있다면 약속은 잡을 없고, 일정이 없다면 그 시간에 약속을 채워넣는다.
바꿔 생각해 보자. 당신은 어떤 자료구조에 새로운 노드를 삽입하고 싶다. 같은 key를 가진 노드를 중복해서 넣을 수 없다. 당신은 먼저 중복을 막기 위해 자료구조를 탐색하고, 중복되는 노드가 없으면 새로운 노드를 삽입할 것이다. 이 과정을 단계적으로 분리한다면 1)서치, 2)비교, 3)삽입 3단계로 나눌 수 있다.
이러한 일련의 과정을 배열이나 힙을 사용하여 구현한다면 조금 비효율적이다.
정렬되지 않은 배열: 서치에 O(n)
정렬된 배열: 삽입에 O(n) -삽입 위치보다 뒤쪽에 있는 요소들을 옮겨야 하므로
힙: O(n) -아래 사진과 같은 상태에서 1을 삽입하려면 모든 요소를 확인해야 할 것이다. 완전정렬 상태가 아니기 때문이다.

반면 BST를 사용하면 O(log n)으로 탐색이 가능하다. BST를 다시 그림으로 살펴보자.

당신은 key가 7인 노드를 찾고 싶다.
1) 루트 노드 8과 비교한다. 7이 8보다 작으므로 왼쪽 서브트리를 본다.
2) 서브트리의 루트 노드 3과 비교한다. 7은 3보다 크므로 이번엔 오른쪽 서브트리를 본다.
이러한 과정을 반복하면 4번만에 7을 찾을 수 있다. 최악의 경우 트리의 높이 h만큼 탐색해야 한다.
참고로 완전이진트리의 최대 노드 개수는 2h-1이니까 시간 복잡도가 O(log n)인 이유는 직관적으로 알 수 있다.
이진탐색트리의 삽입/삭제 연산은 내용이 많아 지금은 다루지 않기로 하고(다음에 여유가 있을때 추가하겠다) 잘 설명된 글을 링크하고 글을 마친다.
https://yjg-lab.tistory.com/139
[자료구조] 이진 탐색 트리 - 탐색, 삽입, 삭제 연산
이진 탐색 트리 이진 트리의 핵심입니다. 탐색 트리는 탐색 작업을 효율적으로 하기 위한 자료구조입니다. 루트 노드를 기준으로 왼쪽 서브 트리의 key값은 루트 노드보다 작고 오른쪽 서브
yjg-lab.tistory.com
'C++ > 자료구조' 카테고리의 다른 글
| --- (0) | 2022.12.04 |
|---|---|
| [자료구조] 그래프와 다익스트라(dijkstra) 알고리즘 (0) | 2022.11.27 |
| [자료구조] DFS(깊이 우선 탐색)와 BFS(너비 우선 탐색) (0) | 2022.11.06 |
| [자료구조] 힙과 우선순위 큐(heap&priority queue) (2) | 2022.09.21 |



댓글